Fibonacci, el matemático que se puso a contar conejos y descubrió la secuencia divina
- Redacción
- BBC News Mundo
El vitral en espiral de la Capilla de Acción de Gracias, Dallas, Texas, Estados Unidos representa la secuencia de Fibonacci.
Durante los siglos en que China, India y el imperio islámico habían estado en ascenso, Europa había caído bajo una sombra.
Toda la vida intelectual, incluido el estudio de las matemáticas, se había estancado.
Pero en el siglo XIII, las cosas estaban empezando a cambiar.
Liderada por Italia, Europa empezó a explorar y comerciar con el oriente.
Con ese contacto llegó la difusión del conocimiento oriental hacia occidente.
Final de Quizás también te interese
Y sería el hijo de un funcionario de aduanas quien se convertiría en el primer gran matemático medieval de Europa.
Una importación mal recibida
De niño, viajó por el norte de África con su padre, donde aprendió sobre los desarrollos de las matemáticas árabes y, especialmente, los beneficios de los números indoarábigos.
Cuando llegó a Italia, escribió un libro que sería de gran influencia en el desarrollo de las matemáticas occidentales.
Fibonacci llevó los números indoarábigos a Europa, pero no fueron bienvenidos.
Ese matemático fue Leonardo de Pisa, más conocido como Fibonacci, y en su "Libro de cálculo", Fibonacci promovió el nuevo sistema de números, demostrando lo sencillo que era en comparación con los números romanos que se utilizaban en toda Europa.
Los cálculos eran mucho más fáciles, algo tremendamente importante para quienquiera que se ocupara de los números, desde matemáticos hasta comerciantes.
No obstante, lo que los números traídos de Oriente despertaron fue desconfianza, no alegría ni alivio.
Los viejos hábitos son difíciles de abandonar.
Los romanos contaban con mucho apoyo.
Algunos creían que estarían más expuestos al fraude, que se prestaban para ser manipulados.
Otros pensaban que eran tan fáciles de usar para los cálculos que le darían poder a las masas, quitándole autoridad a los intelectuales que sabían cómo usar el tipo de números antiguos.
La ciudad de Florencia incluso los prohibió en 1299.
Pero con el tiempo, prevaleció el sentido común, el nuevo sistema se extendió por toda Europa y el antiguo sistema romano se extinguió lentamente.
El enigma de los conejos
Por fin, los números hindú-árabes, de 0 a 9, triunfaron.
Hoy en día, Fibonacci es mejor conocido por el descubrimiento de unos números, ahora llamados la secuencia de Fibonacci, que surgieron cuando intentaba resolver un enigma sobre los hábitos de apareamiento de los conejos.
¡Quién hubiera pensado que contar conejos daría para tanto!
Supongamos que un granjero tiene un par de conejos.
Los conejos tardan dos meses en alcanzar la madurez, y después de eso dan a luz a otro par de conejos cada mes.
El problema era cómo saber cuántos pares de conejos habría en un mes determinado.
Entonces:
- Durante el 1º mes tienes un par de conejos y, como no han madurado, no pueden reproducirse.
- Durante el 2º mes, todavía hay un solo par.
- Pero a principios del 3º mes, la primera pareja se reproduce por primera vez, por lo que hay 2 pares de conejos.
- Al comienzo del 4º mes, el primer par se reproduce de nuevo, pero el segundo par no está lo suficientemente maduro , por lo que hay 3 pares.
- En el 5º mes, el primer par se reproduce y el segundo par se reproduce por primera vez, pero el tercer par es todavía muy joven, por lo que hay 5 pares.
El ritual de apareamiento continúa, pero lo que pronto notarás es que la cantidad de parejas de conejos que tienes en un mes dado es la suma de las parejas de conejos que has tenido en cada uno de los dos meses anteriores, así que la secuencia continúa...
1... 1... 2... 3... 5... 8... 13... 21... 34... 55... y así.
Los favoritos
Resultó que los números de Fibonacci son los números favoritos de la naturaleza.
No solo los conejos los usan.
El número de pétalos en una flor es invariablemente un número de Fibonacci. Si cuentas los segmentos de las piñas hacia arriba y hacia abajo los encontrarás. Incluso los caracoles los utilizan para hacer crecer sus conchas.
Hasta las piñas...
Doquiera que encuentres crecimiento en la naturaleza, encontrarás los números de Fibonacci.
La secuencia de Fibonacci es además es la prima matemática del número áureo, un número que ha obsesionado a la cultura humana durante miles de años.
Número áureo
Si divides cualquier número en la secuencia de Fibonacci por el anterior, por ejemplo, 55/34, o 21/13, y la respuesta siempre es cercana a 1.61803.
Y es por eso que la secuencia de Fibonacci también es conocida como la secuencia dorada, pues ese 1,61803 es lo que se conoce como el número áureo.
Es un número especial que se encuentra al dividir una línea en dos partes, de modo que la parte más larga (a) dividida por la parte más pequeña (b) es igual a la longitud total dividida por la parte más larga.
A menudo, el número áureo se simboliza usando phi, la 21ª letra del alfabeto griego.
En una forma de ecuación, se ve así:
Esos números se pueden aplicar a las proporciones de un rectángulo, llamado el rectángulo dorado, considerado como una de las formas geométricas más satisfactorias visualmente.
El rectángulo dorado también está relacionado con la espiral dorada, que se crea al hacer cuadrados adyacentes de dimensiones de Fibonacci.
Pero para quienes somos principiantes, quizás es más fácil entenderlo si lo pensamos en términos de diseño.
Muchos nombres
El número áureo ha sido descubierto y redescubierto muchas veces, y por eso que tiene tantos nombres: número de oro, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción.
Está en la naturaleza, pero también en las creaciones humanas.
Históricamente, está expresado en la arquitectura de muchas creaciones antiguas.
En la Gran Pirámide de Giza, por ejemplo, la longitud de cada lado de la base es de 230 metros con una altura de 146 metros. La relación de la base con la altura es aproximadamente 1,575, muy cercano al número áureo.
Se cree que Fidias (500 a.C. - 432 a.C.), el famoso escultor y matemático griego, aplicó phi al diseño de esculturas para el Partenón.
De "La última cena" a Twitter
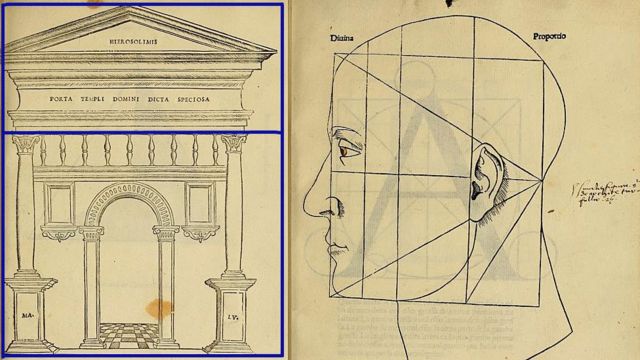
"Sin matemáticas no hay arte", aseguró Luca Pacioli quien, en 1509, publicó "De divina proportione", ilustrado nada menos que por Leonardo da Vinci.
Ilustraciones de "De divina proportione" (la línea azul es agregada, para mostrar la proporción a la que se refieren).
"De divina proportione" es un libro de matemáticas, pero desde la primera página Pacioli afirma que su intención es revelarle a los artistas el secreto de las formas armónicas mediante el uso de la proporción divina.
Y, de hecho, hay quienes piensan que el número áureo es la esencia de la belleza en las proporciones de las pinturas de Da Vinci, quien la llamó sectio aurea.
Aseguran que la usó para definir todas las proporciones en su "Última Cena", "Hombre de Vitruvio" y "Mona Lisa".
"La última cena" con algunos rectángulos áureos como guía. Algunos estudiosos muestran que la proporción se está presente en todas las dimensiones clave, desde las de la sala, la mesa y los escudos ornamentales hasta la posición de los protagonistas.
También se ha notado el empleo de esa divina proporción en obras de Miguel Ángel, Rafael, Rembrandt, Seurat, Salvador Dalí... y hasta en el logo de Twitter.
Lo llevamos por dentro
Pero no hay que siquiera salir de casa para encontrar ese número de oro: nuestros cuerpos y rostros siguen esa proporción matemática.
- La longitud de nuestros dedos, cada sección desde la punta de la base hasta la muñeca es más grande que la anterior en aproximadamente la proporción de phi.
- La medida de la distancia del ombligo humano al suelo y de la parte superior de la cabeza al ombligo es la proporción de oro.
- Una molécula de ADN mide 34 angstroms por 21 angstroms en cada ciclo completo de la espiral de doble hélice. En la serie Fibonacci, 34 y 21 son números sucesivos.
Y, aparentemente, nuestros cerebros están programados para preferir los objetos y las imágenes que usan la proporción divina.
Varios estudios han demostrado que cuando se le pide a voluntarios en pruebas que observen una serie de caras aleatorias, y escojan las que consideran más atractivas -a pesar de no ser mi matemáticos ni físicos familiarizados con el phi- eligen las que muestran proporciones áureas entre el ancho de la cara y el ancho de los ojos, la nariz y las cejas.
Es casi una atracción subconsciente.
Recuerda que puedes recibir notificaciones de BBC News Mundo. Descarga nuestra app y actívalas para no perderte nuestro mejor contenido.
¿Ya conoces nuestro canal de YouTube? ¡Suscríbete!
Fin del contenido de YouTube, 1
https://www.bbc.com/mundo/noticias-46926506






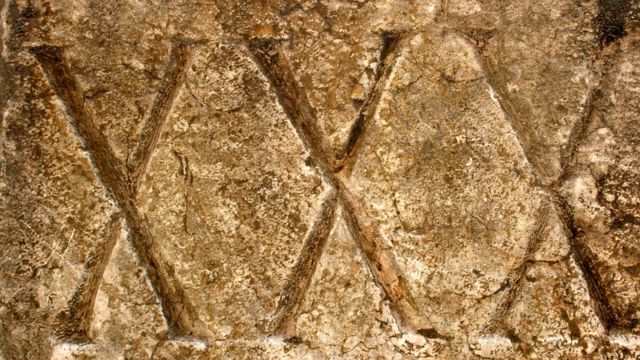


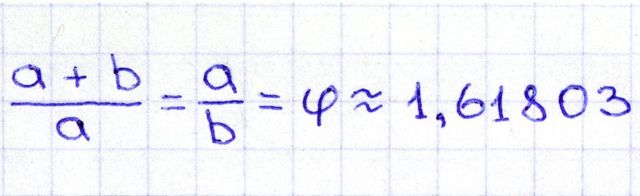







No hay comentarios.:
Publicar un comentario